CRYPTOGRAPHIE C.D.P.

Chiffrage-Déchiffrage en Phase

Auteur: Philippe Lheureux

Résumé des deux grandes méthodes existantes

La cryptographie à clé privée est fondée sur l'utilisation d'une clé unique qui sert tant au chiffrage qu'au déchiffrage des données. Il faut chiffrer le message à l'aide d'une clé , puis faire parvenir séparément au destinataire à la fois le message et la clé de façon à ce que le message ne puisse être déchiffré que par le destinataire prévu. Si la clé est interceptée par espionnage , tous les messages chiffrés avec cette clé seront déchiffrables. De plus et c'est une grosse faille , tous les messages chiffrés avec la même clé finissent par donner des recoupements qui permettent aux experts de décrypter le code. Il faudrait donc changer de clé en permanence mais alors se pose le problème de la transmission de la clé !

La cryptographie à clé publique, d'autre part, utilise deux clés. La première clé demeure privée alors que l'autre est publique. Si l'on utilise la clé publique pour coder un message, la clé privée permet de le déchiffrer. Autrement dit, il suffit de chiffrer le message à expédier à l'aide de la clé publique du destinataire, et ce dernier peut ensuite utiliser la clé privée pour le déchiffrer.

Ici aussi , si l'utilisateur se fait voler sa clé privée , tous les messages chiffrés avec sa clé publique seront déchiffrables. D'autre part , si l'utilisateur distribue des clés publiques , n'importe qui ( même l'ennemi ) peut lui coder un message. Il faut alors rajouter la notion de signature numérique .

J'ai imaginé un système de chiffrage-déchiffrage qui utilise un autre principe .

La clé privée à synchronisation permanente.

Suite à une émission d'ARTE sur la cryptographie ,j'ai eu envie d'inventer une méthode de chiffrage-déchiffrage qui puisse être utilisée sans se soucier des histoires de transmission de clés publiques ou privées et qui assure à coup sur l'identification de l'expéditeur et du receveur ainsi qu'une sécurité maximale des données. En voici le principe détaillé pouvant servir de schéma directeur à un bon programmeur. J'ai même réalisé une application logicielle de cette méthode , contactez moi si vous voulez en savoir plus.

Voici quand même l'exposé de ma méthode :

La grille de chiffrage et de déchiffrage est un tableau informatique de 10x10 dans lequel les caractères du clavier ont été disposés de manière totalement aléatoire.

Les caractères disponibles sont jetés au hasard dans les cases ! A ce stade , inutile de se servir d'un générateur de hasard , votre cerveau peut très bien faire la même chose .

Une case restera vierge pour symboliser l'espace vide entre deux mots. Ainsi l'espace entre les mots ou la ponctuation n'apparaitront jamais directement en clair dans le code mais pourront être codés comme n'importe quel autre caractère.

Grille de chiffrage-déchiffrage

Cette clé est destinée à être stockée sur le disque dur de votre machine sous la forme :

James , Bond ,a,x,1,v,P,6,*,H,g ,& , -------100 caractères en tout dans le meme ordre que la grille de gauche à droite et de bas en haut ---------- u,X,=,<,E,p,L,{,9,K

James Bond est le nom de la personne à qui vous voulez envoyer un message codé. Chaque destinataire sera ainsi identifié avec une clé de 100 caractères derrière son nom. Au départ toutes les clés sont identiques mais vous allez voir plus tard qu'elles se personnalisent très vite toutes seules de telle manière que chaque destinataire aura bien une clé différente d'un autre destinataire.

Coté récepteur , c'est la même chose .. prénom et nom de l'envoyeur suivi des mêmes 100 caractères. Les grilles doivent toujours êtres identiques entre l'émetteur et le récepteur pour que le système fonctionne correctement.

Chiffrage

Dans ce type de grille , chaque lettre peut être codée de multiples manières différentes sans géner pour autant le déchiffrage.

Le logiciel utilise 5 systèmes différents de chiffrage qui se combinent aléatoirement les uns avec les autres sans géner le déchiffrage.

Admettons que vous vouliez écrire le message suivant à la femme de vos rêves qui est comme par hasard mariée à un homme hyper jaloux :-).

 "Béatrice ,téléphone moi à 20h au 01 43 05 24 28 - Luc"

Commencons par la lettre B

Système de chiffrage numéro 1 (LR-LC)

Intersection Lettre-Rangée , Lettre-Colonne.

Dans ce genre de grille , une lettre est toujours à l'intersection de deux autres lettres mais il faut obligatoirement se fixer un sens de lecture pour éviter par exemple que yv ne désigne à la fois le B et le a . Dans notre exemple nous choisirons le sens rangée-colonne. La première lettre est toujours la rangée et la deuxième la colonne .

le B peut donc se coder yv mais aussi y_ yT yQ y3 yR y' yO y< Yv Y_ YT YQ Y3 YR Y' YO Y< Uv U_ UT UQ U3 UR U' UO U< \v \_ \T \Q \3 \R \' \O \< cv c_ cT cQ c3 cR c' cO c< qv q_ qT qQ q3 qR q' qO q< etc...

Ce qui fait 81 possibilités différentes de désigner la même lettre du fait du croisement de 9 lettres horizontales avec 9 lettres verticales.

Si ce système de chiffrage est choisi , le logiciel sort toutes les possibilités de coder une lettre puis en choisi une de manière aléatoire. Exemple cT pour coder B

Système de chiffrage numéro 2 (CR-CC)

Intersection Chaine de lettres Rangée , Chaine de lettres Colonne.

 La lettre B peut aussi être codée par intersection de 2 chaines de caractères de 2 lettres comme yYv_ mais aussi yY_T yYQ3 yY3R yYR' yY'O yYO< YUv_ yU_T yUQ3 yU3R yUR' yU'O yUO< \cv_ \c_T \cQ3 \c3R \cR' \c'O \cO< cqv_ cq_T cqQ3 cq3R cqR' cq'O cqO< etc..

Les inversions de deux groupes de lettres permettent d'étendre encore les possibilités de chiffrage . En effet yYv_ peut aussi s'écrire yY_v , Yyv_ ou Yy_v sans que cela pertube le déchiffrage.

Sur la totalité de la grille et compte tenu des inversions cela fait 64x4 =256 possibilités d'écrire la lettre B avec 4 caractères. Ce système à quand même une restriction en fonction de la position de la lettre à coder . Si elle ne se trouve pas dans le carré de 6x6 au milieu de la grille (exemple C ou X) ce système n'est pas choisi .

Nous verrons plus tard que ce n'est pas vraiment un handicap car chaque lettre codée va bouger de place.

Si ce système de chiffrage est choisi aléatoirement, le logiciel sort toutes les possibilités de coderr une lettre puis en choisi une de manière aléatoire

Exemple: aç3R pour coder B

Ce chiffrage ne se confond pas avec le système de chiffrage numéro 1 lors du déchiffrage car il suffit de tester si les deux lettres sont sur la même rangée et se touchent pour savoir que les deux lettres qui suivent sont sur une colonne.

Une même lettre peut donc être codée sur 2 ou 4 caractères ce qui gêne considérablement le décryptage futur.

En effet car si le texte codé commence par aç3R ... comment savoir s'il s'agit d'une intersection entre a et ç puis entre 3 et R plutôt qu'entre aç et 3R ?

Seul le logiciel possédant la bonne grille de déchiffrage peut s'y retrouver.

Mais ce n'est pas tout car les deux systèmes qui suivent vont encore corser le problème du déchiffrage futur

Système de chiffrage numéro 3 (L-E-L)

Lettre Entre Lettres

On peut aussi désigner la lettre B comme étant comprise entre deux caractères comme U\ ou TQ sans que cela n'interfère avec les systèmes précédents de chiffrage et crée encore plus de flou quand à la disposition réelle des lettres sur la grille. Avec les inversions possibles \U et QT ,cette méthode génère 4 possibilités de chiffrage. Les lettres au pourtour de la grille ne peuvent être codées que verticalement ou horizontalement. Seul les 4 lettres dans les angles du tableau ne peuvent pas être codées avec cette méthode.

U\ ou \U n'est ni une intersection de lettres ni une intersection de chaines mais seul celui qui possède la bonne grille de codage peut s'en rendre compte.

Si ce système de chiffrage est désigné aléatoirement , le logiciel sort deux ou quatre possibilités de cryptage et choisi aléatoirement entre le codage horizontal U\ ou /U et le codage vertical TQ ou QT

Système de chiffrage numéro 4 ( L-E-C)

Lettre Entre Chaines de 2 lettres

Système tiré du système 3 mais qui joue sur le chiffrage à 4 caractères.

La lettre B peut s'écrire YU\c ou _TQ3 mais aussi YUc\ UY\c UYc\ _T3Q T_Q3 T_3Q

Ce qui fait 8 nouvelles possibilités supplémentaire de chiffrage sans problème de déchiffrage.

La aussi , il y a quelques restrictions en fonction de la position des lettres dans le tableau.

Si ce système de chiffrage est désigné aléatoirement , le logiciel sort quatre ou huit possibilités de cryptage et choisi aléatoirement entre les 4 ou 8 possibilités.

Système de chiffrage numéro 5 ( L-D-C)

Lettre de début de chaine

Etant donné que les systèmes précédents n'utilisent jamais la lettre à chiffrer , cette caractéristique peut porter préjudice à la sécurité du code dans le cas exceptionnel d'une suite de lettres identiques.

exemple 1111111111111111111 etc .. donne

h'KëuAI5J-àYc)wh6,bGv'}!ëFgx/IGxd+sO!ùOîs9N4<zhè>u'BKZd=gèu6àB.R^36xD>ujé"àB.P_dJjIzçGHgIs[$o5BpyçC\^GHvVbèLQ$AçL_@ëm8AàègCd_xè;9MkZm0]i.W;xxaSK&l*OsH9++r2kQ<ka^vèJyèOo4$,?#KH=s6(Pù8ëMë:7î%>gîmuH]UéBç]nPN2îhEG3A?#wCaî,ê'çx'ëêt(@K<'êY2rçùW!ëRà2g[îfjpLmo\kBYbét94jKlZ\:#èt#WtcH;pqH@à_gùr6d*LB_/jBExc5@?h=sF#'{'L>J2g20\kbv@_rYàU[)u:j/àêkdzuë\ù{/6"iW':&xRG0CJ]<oJ=='#ilnùS<cOkùYR[{F8a(oi7êP!àI>x0ë{3}YuBF(-pnUzlE+_nJzToCèe^YMWQ-x<Q{yH75Zy?0)6}7î2xj0\5bT_Eeeë{F_j*éu2*"zN[dOnà{+écksTx^T}vUM?R<VOp9+éB-ç\Mù!j{mL:HK&_Bb@pJqB(!i5jbBn52-"tPGsCN4[lO<uxNw!jà}8+wYLKàWnt[2H{Aj$=>VèOx7<=8qèHUP etc ...

ou le 1 n'apparait jamais ! Il serait donc possible de faire la différence entre une suite de 1 et une suite de 0 car si 1 apparait dans le texte chiffré c'est 0 qui est chiffré et vice versa.

idem pour des suites du genre 111F111F111F etc , la lettre qui apparait le moins sera le 1 suivie du F . En faisant une analyse du texte , on pourrait même en déduire la langue employée si le e apparait moins souvent que les autres lettres !

Pour contrer cet effet , le système 5 utilise de temps à autre la lettre chiffrée.

La codification se fait sur 3 caractères

B peut ainsi s'écrire B\c ou BQ3

L'écriture se fait toujours de gauche a droite ou de haut en bas , ce qui fait que ce systeme ne couvre pas la totalité des cases de la grille exemple f , u , 9 et K sont les seules lettres qui ne peuvent pas s'écrire avec ce systeme dans l'état actuel de la grille si dessus .

Lors du déchiffrage , le logiciel analyse si les 3 lettres sont à touche-touche sur la même rangée ou la même colonne et prend la première lettre de la chaine des 3 caractères . Il faut bien entendu faire le test des 4 autres systèmes avant pour éviter tout risque de confusion de système .

Résumons nous :

Pour chaque lettre à coder , le logiciel choisi aléatoirement l'un des 5 algoritmes de chiffrage ci dessus. Pour Béatrice , il peut choisir de coder B sur 2 ,3 ou 4 lettres qui peuvent correspondrent à :

Une intersection de deux lettres - Système LR-LC 2 lettres

Une intersection de deux chaines de deux lettres - Système CR-CC 4 lettres

La lettre comprise entre les deux lettres -Système L-E-L 2 lettres

La lettre comprise entre deux chaines de deux lettres - Système L-E-C 4 lettres

La lettre de début de chaine de 3 caractères continus - Système L-D-C 3 lettres

Le code ainsi produit va considérablement géner les cryptanalystes car il leur faudrait d'abord déterminer quel système de chiffrage a été employé pour chaque lettre.

La phrase "Béatrice ,téléphone moi à 20h au 01 43 05 24 28 - Luc" codée avec le logiciel CDP donne le code suivant

TQè+2CvomyJ'&$Z)w6V&b.wVCSZ)&$DXzV]gN:tSRDL:5Rê"gç07\i4,c*K}kFMBZLSpg2qM9'%;<']P\jYî54i>LvVé8$ZLmq&6Ch@]çyèç.ij!m2a9KLco\8i?oG{=A]i($QèîUb[ub"TYi^(h

mais aussi

_TQ3_è021y2/A{Cqt#%]^4+s$ëVS?!Cx?NymBMVzN?w^gE-;,J*}FPpî$g2\C)qW9',o9x[f\jvézt5içyt.ZL.[Q

%?ms&kALM#à@]B9èç]Pi2j+!rm2a9ét-L:[8îMm){=].WuSMèUbFsEL7g#àKui^E(

Le moteur de chiffrage produit donc un code différent même pour des messages identiques. Dés lors , comment arriver à reconstituer quel système de chiffrage à servi pour chiffrer chaque lettre ?

La premiere lettre s'écrit elle TQ ou TQé+

TQ est elle produit par le système 1 ou le système 3 ?

TQé+ est elle produit par le système 2 ou le système 4 ?

TQé est il un système 5 ?

Le problème va en augmentant avec le nombre de lettres chiffrées !

Prenons 8 lettres TQè+2Cvo et n'oubliez pas que chaque séparation correspond à deux systèmes :-)

Cela fait déja 53 possibilités de séparation des systèmes pour deux lettres chiffrées contre 5 pour une seule ! Les permutations possibles des différents systèmes rendent le code incassable !

De plus , même si l'on arrivait à connaitre le système de chiffrage , il faudrait encore placer correctement les 2 , 3 ou 4 lettres sur la grille et déterminer à quelle lettre elle correspondent ! N'oubliez pas qu'il y a aussi des inversions de lecture pour les systèmes 2,3, 4 et 5.

TQ système 1 peut se placer n'importe ou sur la grille du moment que les lettres T et Q ne sont ni dans la même rangée , ni dans la même colonne.

TQ système 3 peut aussi se placer partout sauf sur les 4 cases aux extrémités de la grille.

et puis comment connaitre la lettre désignée par TQ ?

Le déchiffrage est pourtant simple comme bonjour quelque soit le mode de chiffrage employé . Il suffit tout simplement de posséder la bonne grille de déchiffrage.

Afin d'augmenter la sécurité au maximum , j'ai eu l'idée de combiner cette idée des 5 systèmes de chiffrage avec des permutations des lettres de la grille différentes en fonction de chaque lettre chiffrée.

Chaque case de la grille est associée à un numéro de permutation.

Prenons par exemple la lettre Q située en case 44 .

Table de position des lettres

Si celle ci est chiffrée , la permutation de la table qui s'en suivra correspondra à la permutation 31( voir grille ci dessous ).

Voici l'exemple de la permutation 44 , il y en a 200 différentes dans CDP réparties sur 100 cases . ( 2 par cases . Une pour faire bouger la lettre chiffrée et l'autre pour créer une modification de la grille )

ElseIf numcase = 44 Then 'Permutation 31 échange L5,C4 avec L6,C7 ( ici on voit l'échange entre 31 et 32 )

swapcase(1) = grille(5, 4)

grille(5, 4) = grille(6, 7)

grille(6, 7) = swapcase(1)

'echange L 4 avec L 7 ( pour brouiller des cases supplémentaires à chaque lettre chiffrée )

For i = 1 To 10

swapcase(i) = grille(4, i)

grille(4, i) = grille(7, i)

grille(7, i) = swapcase(i)

Next i

swapcase est un tableau parrallèle qui permet de stocker les données avant de les remplacer par d'autres.

Voici en image le code ci dessus ! Admettons que la lettre Q se trouve sur la case 44 du tableau ci dessus qui correspond a la case 31 du tableau ci dessous , si on la répète plusieurs fois ( QQQQQQQQ etc .. ) elle passera donc en 32 puis en 33 etc. jusqu'a 100 pour revenir à 1 puis 2 puis 3 etc.

Table des permutations

 Ce passage de la permutation 31 à la permutation 32 est associé à une permutation de lignes ( échange lettres bleues avec lettres grises ) mais certaines permutations peuvent aussi être associées à des permutations de colonnes , de demi lignes ou de demi colonnes.Chaque case possède une permutation différente d'une autre. Mon logiciel CDP utilise ce genre de permutations symétriques car il faut pouvoir annuler une permutation en cas d'erreur de saisie d'un caractère mais dans la version finale ou cette interface de démonstration n'existe plus , les permutations peuvent être plus complexes et non annulables .

Voici l'état de la table après cette permutation

La lettre Q a changé de place et certaines lettres de la table ont subit une permutation . Voici par exemple ce que donne une suite du genre

QQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQQ codée suivant ce principe.

0bnMGq;h#.<BW{d5osSQ8mkVv*q5hi"çTaa1<_$QdZFh6ëeS_LO5Tt>z_LvT\Gn^IjvOSh-?Y#D"4NYcà)%TIj_L'#DyçIR?TcV'0LN+>a5jlêi"A+zY-7o+çUèSKgvZlbqMdêY9uùH<dèw#Y^2CTj>Qwt2SGi5rC(Ad>K28Sî6=Kd>y6%+"NêîCgKx5>y#4

Comme la position de la lettre Q varie constamment , son codage est toujours différent ! On remarque aussi la présence de 3Q liés à l'activation du système 5.

Ici vous pouvez remarquer que le premier Q est codé ObnM ( système L-E-C) puis Gq ( système L-E-L choix vertical ) grâce aux tableaux ci dessus.

C'est ainsi que fonctionne CDP et voila pourquoi il est aussi résistant aux méthodes de cryptanalyse. Les lettres n'arretent pas de bouger de place du fait des permutations qui les décalent en tout sens. Un A situé en case 9 peut très bien se trouver en case 27 , 3 lettres plus tard .

L'intérêt de cette méthode de chiffrage est quelle produit un code complètement différent même pour 2 messages identiques. Le tableau de chiffrage se modifie à chaque utilisation et il en va de même pour le tableau de déchiffrage lors de la lecture du message chiffré.

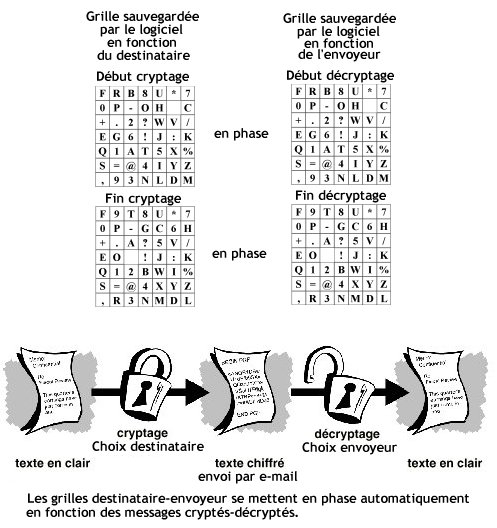
Les logiciels de chiffrage et de déchiffrage se mettent progressivement en phase en fonction des textes chiffrés- déchiffrés. Celui qui n'aurait que la grille de départ n'est pas plus avancé car il lui faut aussi tous les messages transmis pour pouvoir la mettre à jour !

La clé de CDP n'est pas la grille mais le message clair envoyé sous forme chiffré car c'est le message clair qui permet de faire évoluer les grilles en phase . En ce sens CDP apporte quelque chose de nouveau au petit monde de la cryptologie puisque le message et la clé ne font plus qu'un ! Dans tous les systèmes conventionnels , la clé est indépendante du message .. ici c'est le message clair ( avant chiffrage ou après déchiffrage ) qui constitue la clé.

La grille ne constitue que la valeur maximum des permutations possibles . Elle limite les permutations possibles à 100 !

Comment ça marche dans la pratique .

Les deux personnes doivent avoir le même logiciel. Alice veut envoyer un message à Bob.

Alice ouvre son logiciel qui est paramétré sur une grille de chiffrage standard pour tous les logiciels . Celle ci peut évidement être personalisée dès le départ et transmise par courrier AR à Bob pour que Bob paramètre son logiciel en fonction de Alice . En fait , il suffit que Alice et Bob codent une même phrase avant de commencer pour mettre leurs logiciels en phase. Cette phrase peut être la première ligne d'une page d'un livre convenu à l'avance. Il peuvent aussi s'échanger une clé spécifique par courrier. En fait , une simple phrase suffit pour brouiller complètement la grille du fait des permutations liées à chaque lettre codée.

Alice choisi l'adresse du destinataire Bob dans la liste des destinataires.

Alice copie ou tape le texte à coder dans l'interface de chiffrage puis clique sur chiffrage. Le texte se code et la grille de chiffrage de départ évolue en fonction des lettres codées. La grille de code du destinataire Bob est sauvegardée en position 1 . 0= grille de départ standard.

Le fichier codé généré au format TXT par le logiciel de cryptage est joint à un e-mail.

Bob récupère le fichier codé et l'ouvre avec son logiciel en choisissant l'envoyeur Alice dans la liste des envoyeurs.

Il clique sur déchiffrage , le logiciel déchiffre le message en partant de la grille d'Alice en position 0 et sauvegarde la nouvelle grille résultant du déchiffrage en position 1.

Il y a donc mise en phase des grilles entre Alice et Bob pour le prochain envoi à chaque chiffrage - déchiffrage. Alice ne peut communiquer avec Bob que si les grilles de chiffrage - déchiffrage sont en phase. Cela permet d'identifier Alice très sûrement !

Admettons que Alice en soit à son 50 ème envoi et que Bob ne recoive pas ce 50 ème envoi . Bob n'a plus qu'à téléphoner à Alice pour lui demander de reinitialiser son logiciel grâce à la première phrase de la page x d'un livre qu'ils ont en commun et recommencer l'envoi. On peut aussi toujours se servir de la même grille -clé car elle assure déja à elle seule un niveau de sécurité plus que suffisant !

J'ai appelé cette méthode : CDP (Chiffrage Déchiffrage en Phase ) et j'aimerais connaitre votre avis en ce qui concerne cette méthode qui permet de s'affranchir des notions de clé privées ou publiques.

Ce qui m'intéresse surtout c'est le coté sécurité ! Est il possible de reconstituer la grille de départ d'un message chiffré autrement que par une attaque à force brute ? Je pense que non vu que seuls 2 ou 4 caractères sur 100 sont transmis pour chaque lettre chiffrée et que la table se modifie complètement entre chaque lettre . On ne sait même pas à quoi correspondent les caractères transmis à cause du choix aléatoire des méthodes de chiffrage.

Qu'en pensez vous .. vulnérable ou invulnérable ?

Liens :

D' après un contact sur fr.misc.cryptologie , il semble qu'une partie du principe que j'ai imaginé à déja été imaginé par un ingénieur cryptologue américain qui l'a publié dans Cryptologia, volume XIV, numéro 4, d'octobre 1990.

Le principe de cryptage est totalement différent mais le brouillage de la grille est du type "substitution dynamique" .

http://www.dean.usma.edu/math/pubs/cryptologia/

Et on peut lire l'article sur son site web:

http://www.ciphersbyritter.com/ARTS/DYNSUB2.HTM

Je suis content d'avoir eu le même genre d'idée pour le brouillage de la grille après utilisation car finalement , ce qui m'importe le plus c'est d'en avoir eu l'idée sans avoir lu quoi que ce soit sur le sujet.

Quand je pense que sur fr.misc.cryptologie , certains internautes se sont foutus de moi en disant que mon système était facilement cassable et tout juste 'bon à communiquer avec ma petite soeur ' j'en rigole encore :-)

D'ailleurs , je leur lance un défi !

Voici une phrase de 5 mots dont deux sont identiques .

u>Xàz7HçlqfGhîl!u0^nErz7kL5-d[^b<@X>NaO1ê#EUGFm-8Cgz1L(VZJb&î^D*

 Elle a été chiffrée avec mon logiciel CDP à partir d'une grille connue de moi seul . J'offre une bouteille de champagne demoiselle + un livre "Lumières sur la lune" dédicacé à celui qui sera capable de me retrouver les mots en question .

Bonne chance :-)

VISITEURS